Date: 15 Jan. (Thu.)
Place: West Wing, 6th floor, Colloquium Room and on the Web (zoom)
Time: 17:00-19:15
- Speaker 1: Yuma Tamura(Ritsumeikan University)
- Time:17:00-18:00
- Title: Affine過程の表現公式と部分積分公式
- Abstract:
本講演では,次の確率微分方程式で定義される拡散型のAffine processを扱う:
\[
dX^x_t = \sqrt{ \alpha X^x_t } \,dW_t + ( \beta X^x_t + b )dt,\quad X^x_0=x.
\]
ここで,\(W\)は\(1\)次元Brown運動であり,\( \alpha > 0 \), \( \beta \in \mathbf{R} \), \( b \ge 0 \)は定数のパラメータである.Affine processのクラスは,代表的な金利モデルであるCox–Ingersoll–Ross (CIR)モデルを含むため,数理ファイナンスにおいて重要である.
本研究では,テスト関数\(f\)に対し,期待値の初期値\(x\)による微分
\[
\partial_x E[ f(X^x_T) ]
\]
の表現公式および部分積分公式を導出する.特に前者は,数理ファイナンスにおける「オプションのデルタ」に対応し,実務的な応用可能性を持つ.
また,本講演ではこれらの公式の発見の端緒となったsquared Bessel processに関する考察についても述べる.
さらに,学生に向けて,最初にsquared Bessel processの基本事項の解説も行う予定である.
なお,本講演の内容はArturo Kohatsu-Higa氏(立命館大学)との共同研究に基づく.
- Speaker 2: Takuya Nakagawa (Ritsumeikan University)
- Time:18:15-19:15
- Title: $L^{\alpha-1}$ distance between two one-dimensional stochastic differential equations with drift terms driven by a symmetric $\alpha$-stable process
- Abstract:
This paper develops a quantitative stability theory for one-dimensional SDEs with non-zero drift and time-dependent coefficients, driven by a symmetric $\alpha$-stable process for $\alpha\in(1,2)$. We establish the first explicit convergence rates for this broad class. Our main result is a H\”older-type estimate for the $L^{\alpha-1}(\Omega)$ distance between two solution paths, which quantifies stability with respect to the initial values and coefficients. In this estimate, the distance between coefficients is measured by a weighted integral norm constructed from the transition probability density of one of the solutions. The proof is based on a refined analysis of a mollified auxiliary function, for which we establish a new, sharper derivative estimate to control the drift terms.
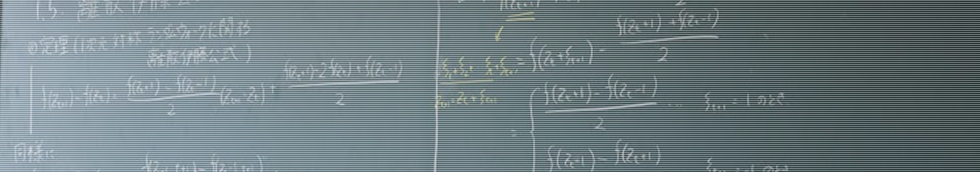

 日本語
日本語 English
English