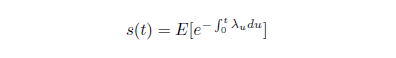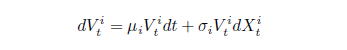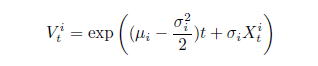本小節では、1-ファクターガウシアンコピュラモデルの自然な拡張の一つである1-ファクター・ダブル
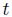
・コピュラ・モデルについて間単に説明する。このモデルは、Hull氏とWhite 氏により2004 年に提案された方法である。
このモデルでは、標準正規分布の代わりに、より分布の裾が重い(ファット・テイルな) 分布である
標準化された(スチューデントの)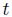 分布(normalized Student's t distribution)
分布(normalized Student's t distribution)を適用するモデルである。つまり、等式(2) の2 つの確率変数
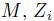
が以下のように標準化された(スチューデントの)
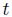
分布を持つ確率変数と仮定したモデルである:
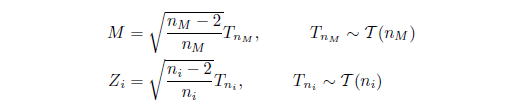
ここで、
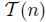
は、自由度
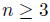
の(スチューデントの)
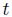
分布である。
このモデルでは、確率変数
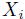
が陽に表現できない。よって数値シミュレーションを行う必要がある。
コピュラ・モデルの問題点
コピュラ・モデルの問題点として、dynamic ではない点やパラメータのキャリブレーションが不安定である点などが挙げられる。
本小節では、リスク中立確率測度の存在については仮定し、あるリスク中立確率測度
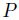
が与えられているものとする。
デフォルトを表現するモデルには、構造モデルと誘導(reduced-form) モデルという2 つの主要なモデルがある。構造モデルは、債権や資産価格のような企業の構造変数の計算方法を用いる。あとに説明するマートンモデルは、デフォルトに関する最初の現代的なモデルであり、最初の構造モデルである。構造モデルは、企業の信用力や企業の状態、企業の財務状況に依存して与えられる。ゆえに外因的な要因よりも内因的な要因によりデフォルトが起こるという考えに従うモデルである。一方、reduced-form(誘導)
モデルは、
デフォルトと企業価値の間の関係を考慮しない。構造モデルとは対照的に、reduced-form(誘導) モデルでのデフォルト時刻は、企業価値で決定されるのではなく、外因的に与えられたジャンプ過程(ポアソン過程、コックス過程など。)の最初に起こるジャンプによって決定される。ハザード率を統治するパラメータは、市場データから推定される。CDO のモデリングを考える際、複数の銘柄からCDO が構成されるので、参照資産のデフォルト時刻の同時分布を考える必要がある。よって、モデル化を行う際、デフォルト相関についても扱うべきである。さらに実際のデータに現れる現象として、デフォルト分布の裾の部分が正規分布の裾よりも太くなることが経験的なデータ分析の結果報告されている。このことをテイル(裾)が厚くなるということから
ファット・テイル現象という。この現象についても考慮する必要がある。以下で、簡単にそれぞれのモデルについての簡単な説明や問題点について述べる。
構造モデルは、モンテ・カルロ・シミュレーションによって、実行される。つまり、高次元確率微分方程式に関するシミュレーションの問題がある。さらに流動性の問題からCDS
スプレッドがジャンプする場合があり、ジャンプも考慮したモデルを考え、デフォルト発生のメカニズムを考察できるモデルにするべきであるが、キャリブレーションの問題として、ジャンプ過程(Lévy
過程) として何を採用すべきか、どのようなリスク中立確率測度を採用すべきかを検討する必要がある。もちろん、高次元ジャンプ型確率微分方程式に関するシミュレーションの問題もある。
ブラック-コックス・モデルでは、マートン・モデルでの問題点を改善するために、企業
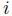
のデフォルトが
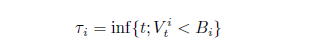
で起こるものとする。これは、
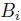
を下回った最初の時刻でデフォルトが発生するということを意味している。マートン・モデルより明らかに取り扱いが難しいモデルとなっているが、デフォルトに関する意味が直感的にも経済的にも理解しやすいモデルである。
本小節では、マートン・モデルについて説明する。各企業は、時刻
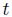
で清算するものと仮定し、企業
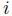
に対するデフォルト境界を
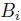
で表すものとする。つまり、企業価値
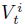
が境界
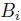
を下回ったときデフォルトと定義する。(
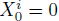
としても一般性は失わない。) ブラウン運動
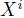
は、
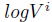
に伊藤の公式を用いることにより、
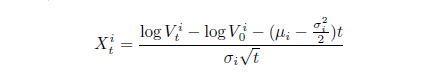
と表すことができる。そして、
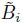
を
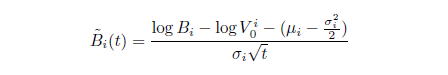
とすると、企業価値
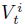
が境界
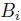
を下回ることは、ブラウン運動
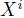
が
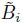
を下回ることと同値である。すなわち、ブラウン運動
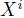
が
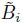
を下回ったときデフォルトが発生すると言い換えることができる。これにより、時刻
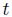
での企業
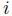
のデフォルト確率は、
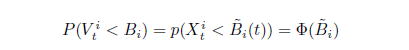
と表現できる。
マートン・モデルの問題点としては、満期
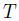
以前に資産価値が低下してもデフォルトしない状況が起こりうることである。満期が異なる複数の債権を扱った場合、過去に倒産した企業がその後生存している状況が起こりうる。過程が強く現実的な動きをしているとは言えない場合がある。
サブプライム問題以前は、1-ファクターコピュラモデルの中でも、もっとも実務で用いられていた基本的なモデルであるガウシアンコピュラモデルについて、本小節では説明を行う。ガウシアンコピュラは、等式2
の2 つの確率変数
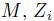
を標準正規分布に従う確率変数と考えたモデルである。このとき確率変数
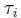
の分布関数を
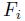
とすれば、
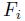
は、狭義単調増加関数であり、
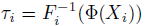
となることに注意する。状態変数
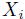
の同時分布について考える。任意の
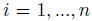
に対して、銘柄
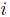
のデフォルト確率を考えると、
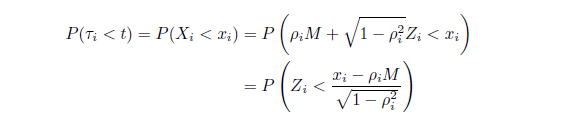
となる。ここで仮定より
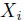
が標準正規分布に従うことに注意する。よって、標準正規分布の分布関数を
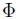
とすると、
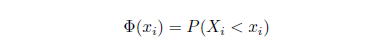
と表すことができる。このことから、
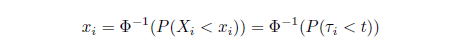
と表すことができる。したがって、銘柄
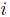
のデフォルト確率は、
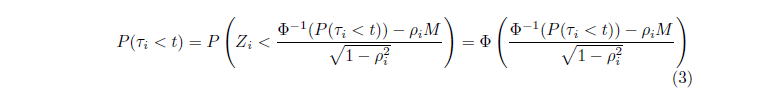
となる。次に
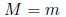
と条件付けた確率を考えると、
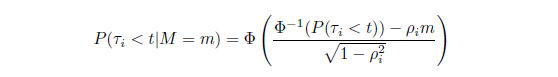
となる。ここで、
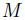
と
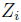
は、互いに独立であり、さらに異なる銘柄
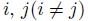
に対して、確率変数
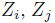
は互いに独立であることを思い出すと、デフォルト時刻
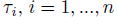
の同時分布は、
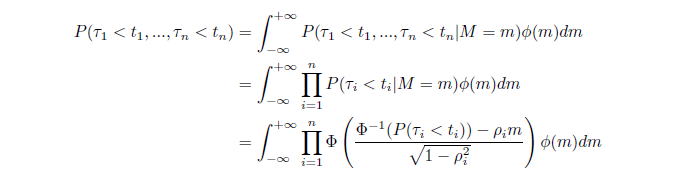
となる。ここで、関数
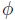
は、標準正規分布の確率密度関数である。
このように、1-ファクター・ガウシアン・コピュラ・モデルでは、デフォルト時刻の同時分布が単純な式で表現できる。さらに
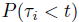
を与えることにより、被積分関数が解析的に計算できる。よって、デフォルト時刻の同時分布を求めるには、変数
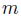
に関する積分の数値計算を行うだけである。以上がガウシアン・コピュラ・モデルの簡単な説明である。
ガウシアン・コピュラの問題点:
デフォルトに関する現実のデータに現れる現象として、デフォルト分布の裾の部分が正規分布の裾の部分よりも太くなることが経験的なデータ分析の結果から報告されている。このことをテイル(裾)が厚くなるということからファット・テイル現象という。標準正規分布に従うガウシアン・コピュラモデルでは、ファット・テイル現象を表現できていないので、現実のデフォルトを表現するモデルとしては、不十分であると考えられる。このことについては、分布の裾を厚くするために、標準確率分布に従う確率変数を用いず、他の分布を用いる研究がされている。例えば、以下で説明する1-ファクター・ダブル
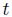
・コピュラ・モデルなどがある。
シミュレーション・サブグループの研究背景
ここでは、上記で説明したモデルよりデフォルトの特徴を考察することが可能である構造モデルについての簡単な説明を行う。
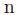
個の銘柄を参照資産とするCDOを考える。企業
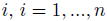
の企業価値が確率微分方程式
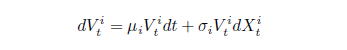
で表現されているとする。ここで、
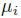
は、企業
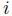
の企業価値の期待成長率を表すパラメータであり、
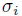
が企業
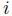
のボラティリティ、つまり企業価値の変動の激しさを表すパラメータである。さらに、第二項は、ノイズ項であり、
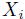
は、
ブラウン運動(ホワイトノイズ)に従うとする。このとき、確率微分方程式は、陽に解を持ち、
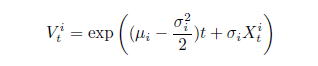
となる。このように構造モデルでは、企業の価値をモデル化している。
注意:
構造モデルでは、株価過程から構成されるアセット測度、リスク中立測度、実測度の3 つの測度による評価がそれぞれ考えられる。
大阪大学 金融・保険教育研究センター(CSFI)
Copyright © 2010 JST/CREST コハツ・チーム
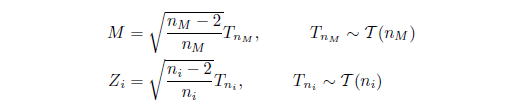
![]() で表すものとする。
で表すものとする。![]() を時刻
を時刻![]() から見て時刻
から見て時刻![]() で生存する確率とする。これを生存確率と呼ぶ。
で生存する確率とする。これを生存確率と呼ぶ。![]() をデフォルト時刻とすると、生存確率
をデフォルト時刻とすると、生存確率![]() は、
は、![]()
![]() まで発生していないとき、次の瞬間にデフォルトが起こる確率は、
まで発生していないとき、次の瞬間にデフォルトが起こる確率は、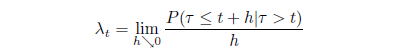
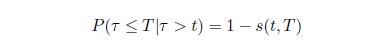
![]() は、条件付生存確率とよばれるもので、
は、条件付生存確率とよばれるもので、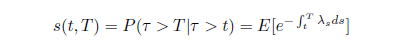
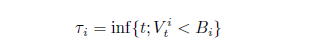
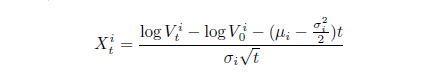
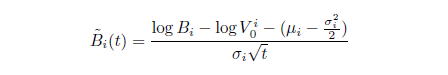
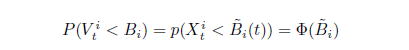
![]() を銘柄
を銘柄![]() のデフォルト時刻とし、intensity
のデフォルト時刻とし、intensity![]() のpoisson 過程に従うものとする。銘柄
のpoisson 過程に従うものとする。銘柄![]() の状態をあらわす変数を平均0、分散1 のある確率変数
の状態をあらわす変数を平均0、分散1 のある確率変数![]() で表現する。このとき、
で表現する。このとき、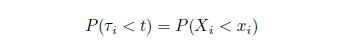
![]() が存在する。このとき、銘柄
が存在する。このとき、銘柄![]() の状態を表す確率変数
の状態を表す確率変数![]() がある境界
がある境界![]() を下回った時、時刻
を下回った時、時刻![]() までに銘柄
までに銘柄![]() がデフォルトするということを意味している。1-ファクター・コピュラ・モデルでは、この状態を表す確率変数
がデフォルトするということを意味している。1-ファクター・コピュラ・モデルでは、この状態を表す確率変数![]() が2つの確率変数の和で
が2つの確率変数の和で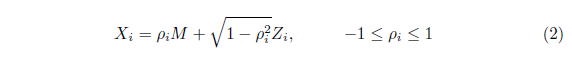
![]() は、市場の共通ファクターであり、確率変数
は、市場の共通ファクターであり、確率変数![]() が銘柄
が銘柄![]() の固有ファクターである。このとき
の固有ファクターである。このとき![]() と
と![]() は、互いに独立であり、さらに異なる銘柄
は、互いに独立であり、さらに異なる銘柄![]() に対して、確率変数
に対して、確率変数![]() は互いに独立であるとする。このことから、
は互いに独立であるとする。このことから、![]() のとき、銘柄
のとき、銘柄![]() と銘柄
と銘柄![]() の状態を表す確率変数
の状態を表す確率変数![]() の
の![]() である。
である。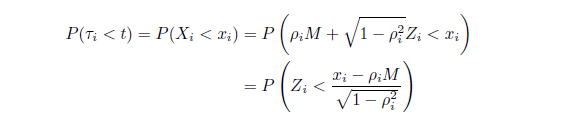
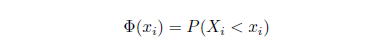
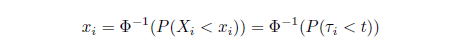
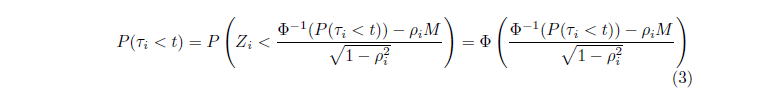
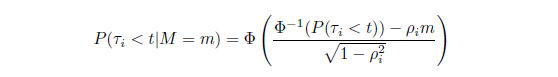
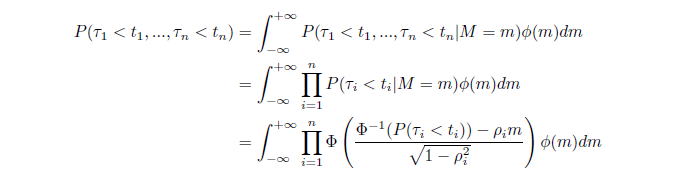
![]() によりモデル化されているとする。Intensity(強度) モデルでは、デフォルト時刻は、与えられたintensity(強度)に関するポアソン過程の最初のジャンプが起こる時刻であるから、デフォルト時刻
によりモデル化されているとする。Intensity(強度) モデルでは、デフォルト時刻は、与えられたintensity(強度)に関するポアソン過程の最初のジャンプが起こる時刻であるから、デフォルト時刻![]() は、
は、![]()
![]() の強度を
の強度を![]() とすると、生存確率は、
とすると、生存確率は、![]()
![]() と考えることにより、より一般化することができる。(コックス過程など。) このとき、生存確率は、
と考えることにより、より一般化することができる。(コックス過程など。) このとき、生存確率は、